Pierre CRESPIN (eNETetMATHS)
Etude sur le quinzième pavage pentagonal du plan,
2020 Réponses
Réponses à Pourquoi? du moins tentatives de réponses, car, s'il me semble avoir un peu progressé, je n'en suis toujours pas bien convaincu. (Travaux en cours)

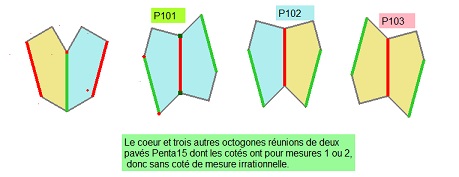
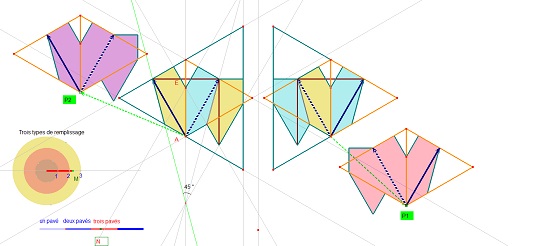
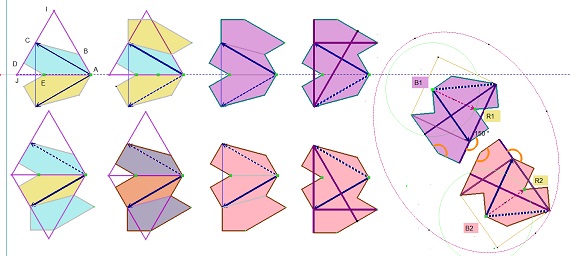
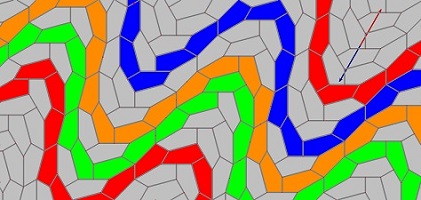
Que le pavé pentagone Penta15 soit inscriptible dans un triangle équilatéral et que tous ses angles soient multiples de 15° (ou pi/12), ainsi que de très nombreux angles liés à des figures plus complexes associées au pentagone Penta15, ou à plusieurs Penta15 accolés, est une première propriété fondamentale. Ce pi/12 est la clé de la réussite pour ce pavé. Il est d'ailleurs aussi inscriptible dans des triangles isocèles (10pi/12,pi/12,pi/12) ou des losanges ((10pi/12,2pi/12) très présents dans diverses figures. Cliquez sur la figure ci-dessous pour le voir.
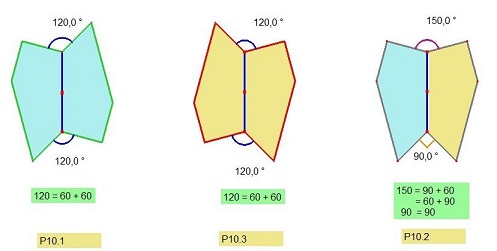
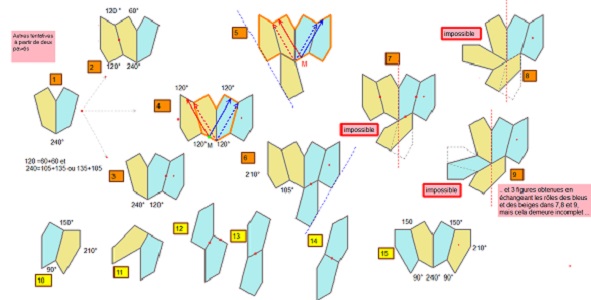
L'étude faite à propos de la somme de 2 ou 3 angles conduit à remarquer que 120° ne se décompose qu'en 60°+60°, ce qui facilitera la recherche de la poursuite du pavage, que 75° ne figure pas dans la liste des angles et de leurs sommes, et enfin qu'il ne peut y avoir deux angles 135° et 150° adjacents puisque 285° a 75° pour supplément à 360° et donc que cet angle libre ne pourra être rempli exactement.

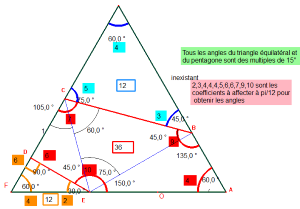
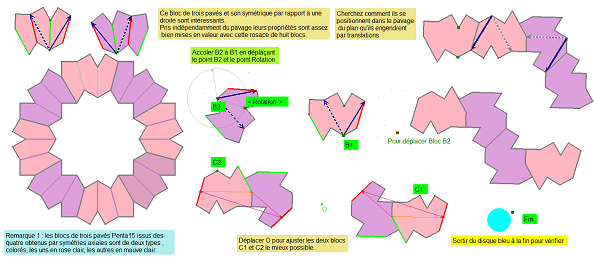
Cliquez ici pour voir des angles de 15° dans le bloc de 3 pavés. et là pour d'autres propriétés.
Assembler les pavés Penta15 (droits ou gauches) de préférence en privilégiant les grands côtés ( côté "2" AE et côté irrationnel BC ou "0" ou "ir") me parait assez naturel (meilleure stabilité du contact et peut-être aussi une avancée plus rapide dans la recherche du pavage pentagonal du plan ?) et peut-être aussi privilégier les symétries axiales?
De plus, vu les mesures des côtés (1,2,ir,1,1) , et en obligeant à priori un contact côté à côté et sommet à sommet, si cela est possible, ce qui incite à ne pas privilégier le 2 = 1 + 1 sans l'exclure, le choix est réduit : "2" sur "2" (vert sur vert), "ir" sur "ir"(rouge sur rouge), mais de deux manières :
- par symétrie axiale ( deux pavés de couleurs différentes) ou
-par symétrie centrale par rapport au milieu du coté (deux pavés de même couleur), donc six possibilités présentées ci-dessous.

Avec une nouvelle symétrie axiale à partir d'un coeur, on obtient un 3° pavé de deux manières. On obtient 2 blocs de 3 pavés assez intéressants, qui engendrent le pavage. Ces deux blocs s'assemblent de deux manières au moins, et ce, de façons très différentes pour le résultat.

On va le voir très rapidement comme ci-dessous. On reviendra sur ce point plus tard..

Ces deux pavés, symétriques orthogonaux l'un de l'autre, pavent le plan en mettant en évidence des directions privilégiées suivant le choix des couleurs des blocs, comme on peut le voir ci-dessous. Mais on verra aussi, si ce n'est déjà vu, que l'on peut faire apparaitre d'autres formes dont des "vagues" et sinusoïdes, avec d'autres blocs générateurs.
On peut aussi poursuivre par une symétrie axiale à partir d'une autre paire que le coeur, soit P101, P102, P103

ou bien encore poursuivre avec une symétrie centrale dont le centre est le milieu du côté "2" ou du côté "ir".

A approfondir pour les deux paires ayant un centre de symétrie, puisqu'ainsi apparait un angle de 120° (60+60), donc 2*2 possibilités,
avec une symétrie centrale potentielle!

Ces divers cas sont plus ou moins déjà étudiés par ailleurs mais il faudrait en donner un résumé ici.
Les figures ci-dessous sont censées donner un éclairage sur certaines propriétés.

2019 construc5 40.html
2019 penta 764new.html
2019 Blocs 123ter.html
2019 New Penta15 qua.html


2019 Blocs 123ters.html à vérifier


2019 Blocs 123 Penta15 plus.html à vérifier

2019 Blocs 3Penta15 n.png

Les blocs présentés plus haut (ou le bloc utilisé recto ou verso) pavent le plan de manière assez régulière.
Leur assemblage est en partie justifié par des considérations de symétries qui ne sont pas toujours évidentes à priori en ce qui concerne deux blocs d'orientations différentes.


Voir ces propriétés illustrées par une figure Cabri.

Voir les diverses facettes du pavage engendré par ces blocs générateurs ou Autre Blocs, autres pavages

Si besoin : Questions Réponses Pourquoi? ImagesReponses ou Aller plus vite à la conclusion
Autres blocs ...
autres formes du pavage
ImagesReponses